Факультет почвоведения. 2 курс (осенний
семестр)
Редакция 2001 года.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ К
КОЛЛОКВИУМУ №I
«Кинематика
и динамика материальной точки»
1. Описание движения
материальной точки в координатной и векторной формах. Перемещение, скорость.
Тангенциальное и нормальное ускорения.
2. Движение, точки по
окружности. Угловая скорость. Угловое ускорение. Преобразования Галилея.
Классический закон сложения скоростей.
3. Взаимодействие тел.
Первый закон Ньютона. Инерциальные и неинерциальные системы отсчета. Понятия
силы, массы, импульса. Второй закон Ньютона. Дифференциальные уравнения
движения материальной точки.
4. Силовые поля.
Гравитационные силы. Закон всемирного тяготения. Движения планет и
искусственных спутников Земли.
5. Сипы инерции.
Центробежная, сила инерции, ее проявления на поверхности Земли. Понятие о силе
инерции Кориолиса.
6. Центр
масс системы материальных точек и закон его движения.
ЗАДАЧИ
1.
Материальная точка двигается па окружности с ускорением вокруг оси ОХ.
Показать на чертеже вектора R (радиус-вектор точки), v, a, an,
at, w, b (угловое ускорение).
2.
Определить линейную скорость v и центростремительное ускорение an точек, лежащих на земной поверхности: а) на
экваторе ( Rз =6,37 *
106
м); б) на широте Москвы (j = 560).
3. Тело
массы m двигается под действием силы F(Fx,0,0),
Определить закон движения (х=x(t) , у=у(t),
z=z(t)), если в момент времени t=0 тело имело координаты x0
,у0 ,z0, и скороcть V(Vx0, Vy0, Vz0).
4. Груз
массы m висит на пружине, упругость которой k. В момент времени t= 0 груз, оттянутый на величину Dx вниз, отпускается. Определить закон движения груза
в последующие моменты времени.
5.
Определить разность ускорений свободного падения тел на полюсе и на экваторе
Земли (Rз =6,37 * 106 м).
Контрольные
вопросы и задачи по коллоквиуму №2
«Законы
сохранения. Колебания. Волны.»
1. Закон сохранения импульса
для системы материальный: тачек.
2. Работа сил. Потенциальные
силы. Кинетическая и потенциальная энергии. Закон сохранения энергии в механике.
3. Динамика вращательного
движения. Момент инерции точки, массивного тела (обруч, диск, стержень).
4. Момент импульса. Момент
силы. Закон сохранения момента импульса. Гироскопический эффект.
5. Уравнение гармонического
осциллятора. Собственные и вынужденные колебания. Явление резонанса.
6. Уравнения плоской
и сферической упругих волн. Амплитуда, частота, фаза волн.
Стоячие и бегущие волны. Перенос энергии упругими волнами.
ЗАДАЧИ
1. В лобовом столкновении протон(относительная масса равна I), движущийся со скоростью 3*10 м/с, сталкивается с неподвижным ядром гелия (относительная масса равна 4) и отскакивает точно назад со скоростью 1,8*107 м/с. Какую скорость приобретет ядро гелия при абсолютно упругом ударе?
2.
При какой минимальной скорости v0 , сообщенной ракете при
запуске вертикально вверх, она удалится от поверхности Земли на расстояние,
равное радиусу Земли (Rз= 6,37*106 м).
3.
Рассчитать момент инерции обруча, сплошного тонкого диска (радиус R ,
масса m), тонкого стержня (длина l, масса m) относительно оси,
совпадающей с осью симметрии (для стержня - ось, проходящая через его середину
и перпендикулярная длине стержня).
4.
Диск радиуса R свободно подвешен на горизонтальной оси, проходящей
перпендикулярно его плоскости через середину радиуса. Определить период
колебаний диска на оси.
5.
На горизонтальную ось насажен шкив радиуса R . На шкив намотан шнур, к
свободному концу которого подвешена гиря массы m. Считая массу шкива равномерно
распределенной по ободу, определить ускорение, с которым будет спускаться гиря,
и натяжение нити.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ К КОЛЛОКВИУМУ №3
"Молекулярно-кинетическая теория и термодинамика"
1. Идеальный газ. Давление,
объем, температура. Основное уравнение молекулярно-кинетической теории газов.
2.
Распределение молекул по скоростям (распределение Максвелла) и координатам
(распределение Больцмана).
3. Явления
переноса: диффузия, теплопроводность, внутреннее трение.
4. Внутренняя
энергия идеального газа. Степени свободы молекул и закон о равнораспределении
энергии по степеням свободы. Первый закон термодинамики.
5.
Равновесное состояние и основные равновесные процессы в идеальном газе.
6. Второй
закон термодинамики. Энтропия и её статистическая интерпретация. Особенности
термодинамики открытых систем.
7.
Реальные газы и жидкости. Уравнение Ван-Дер-Ваальса. Поверхностное натяжение
жидкости. Капилярные явления. Формула Лапласа.
ЗАДАЧИ
1.
Углекислый газ СО2 массой 10г нагрет от 20 до 30 °С при постоянном
давлении. Найти работу расширения газа и изменение его внутренней энергии.
2.
Используя распределение Максвелла, найти, каково отношение числа молекул,
имеющих энергию 2<W> ,
к числу молекул с энергией <W>; (<W>=<mV2/2>=3/2 kБT)
3. Частичка
пыли диаметром 10 мкм имеет объем 10-15 м3 и плотность,
близкую к плотности воды. Какова средняя скорость такой частички при комнатной
температуре (конвекция отсутствует, средняя кинетическая энергия частички 3/2 kТ).
4.
В каком случае изменение давления газа будет большим: при сжатии его на
определенную величину в теплонепроницаемой оболочке или при изотермическом
сжатии?
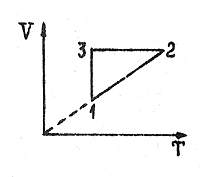
5.
С некоторым количеством идеального газа совершается цикл 1-2-3-1, изображенный
на рисунке в координатах V-Т.
Изобразить тот же процесс на графике зависимости давления от объема и
определить, на каких стадиях процесса газ получал, а на каких - отдавал тепло.